Linear Time-invariant System Examples

Time-invariant systems are systems where the output does not depend on when an input was applied. YnH xn ynrH xnrr. Solve first- second- and higher-order linear time-invariant LTI or-dinary differential equations ODEs with forcing using both time-domain and Laplace-transform methods. Effect of time-scaling on the time variance property of a. Linear time-invariant system theory is also used in image processing where the systems have spatial dimensions instead of or in addition to a temporal dimension. In linear time-invariant systems the system response is always predictable no matter when it occurs or at what frequency it occurs. Simple examples of linear time-invariant LTI systems include the constant-gain system yt 3 xt and linear combinations of various time-shifts of the input signal for example.

In a time-invariant system both outputs would be identical except that the one in Figure would be delayed by t 0 t 0.

Computing the ZSR - example 1. Linear systems are systems whose outputs for a linear combination of inputs are the same as a linear combination of individual responses to those inputs. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features. One has to specify all the. Linear Time-Invariant LTI Systems - YouTube. If the linear system is time invariant then the responses to time-shifted unit impulses are all time-shifted versions of the same impulse responses.

Introduction To Linear Time Invariant System Descriptions Youtube

Linear time-invariant system examples. The system which is linear and time-invariant is called linear time invariant LTI system. While these properties are independent of linearity and time invar-iance for LTI systems they can be related to properties of the system impulse response. Of course here it is easy to.

Most of the systems in the nature are LTI systems. Solve first- second- and higher-order linear time-invariant LTI or-dinary differential equations ODEs with forcing using both time-domain and Laplace-transform methods. Recall that the dierence equationy 7f3y corresponds to the above system.

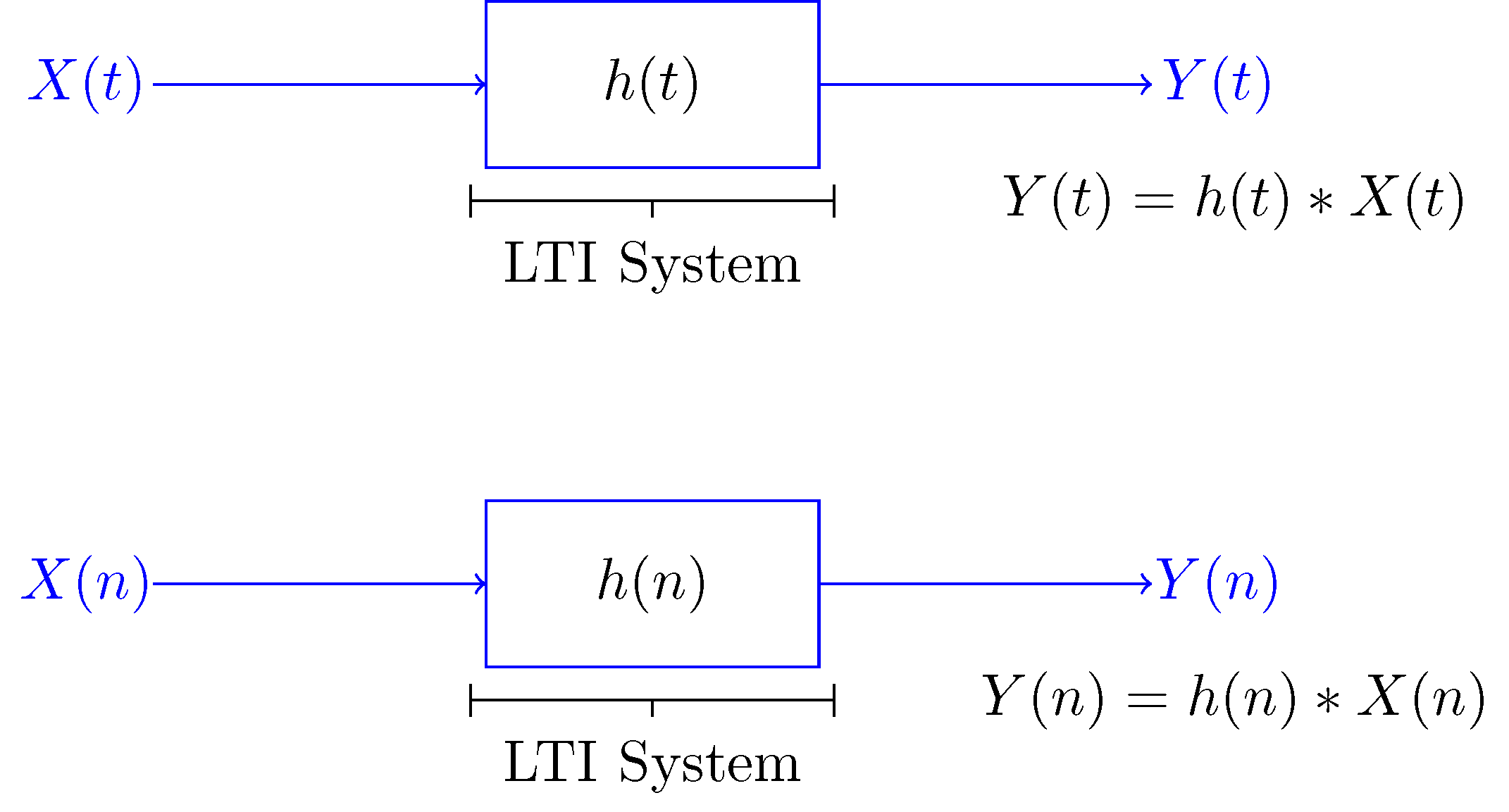
Characterization of LTI Systems. Linear time-invariant systems LTI systems are a class of systems used in signals and systems that are both linear and time-invariant. I yt txt.

In linear time-invariant systems the system response is always predictable no matter when it occurs or at what frequency it occurs. H αu nβv α u β v Time Invariant. Simple examples of linear time-invariant LTI systems include the constant-gain system yt 3 xt and linear combinations of various time-shifts of the input signal for example.

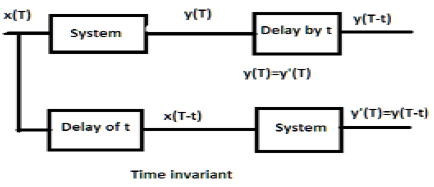
Yn xn2 is not linear since 2yn 2xn2 does not reduce to yn xn2. A system is called time-invariant if a time shift in the input signal xt t_0 causes the same time shift in the output signal yt t_0 it is shown in Figure 2. Because the system TI is time-invariant the inputs x t x t and x t t 0 x t t 0 produce the same output.

Yn 3xn is linear since doubling it yields 2yn 6xn 2yn 32xn. The major classifications of a digital system are Linear and Non Linear systems Time Invariant and Time Variant systems Causal and Non Causal. In a time-invariant system both outputs would be identical except that the one in Figure would be delayed by t 0 t 0.

Effect of time-scaling on the time variance property of a. As it burns tremendous amount of fuel the mass reduces quickly over short periods of time.

Linear Time Invariant Lti Systems Youtube

Linear Time Invariant Lti Systems With Random Inputs

A A Linear Time Invariant Lti System Takes An Input Signal And Download Scientific Diagram

Linear Time Invariant System What Is A Lti System Lti System Superposition And Time Invariance Youtube

A Linear Time Invariant System Is Characterized By Its Impulse Download Scientific Diagram

Stochastic Processes Lecture 7 Linear Time Invariant Systems

Systems

Linear Time Invariant And Causal Systems Youtube

Sample Solution To Example Set 3 Linear Time Invariant Systems In

Linear Time Invariant System Wikipedia

A A Linear Time Invariant Lti System Takes An Input Signal And Download Scientific Diagram

Linear Time Invariant System Wikipedia

Chapter 2 Time Domain Representation Of Linear Time

Solved Problem 5 10 Pts A Linear Time Invariant System Chegg Com

Chapter 4 Transfer Function And Block Diagram Operations 4 1 Linear Time Invariant Systems 4 2 Transfer Function And Dynamic Systems 4 3 Transfer Ppt Download

Sample Problems And Important Short Answers Linear Time Invariant Discrete Time Systems

Invertibility Of Linear Time Invariant Systems Digital Signal Processing Lecture 20 Slides Electrical And Computer Engineering Docsity

Discrete Time Linear Time Invariant Systems Sections Ppt Video Online Download

Solved Problem 4 Consider The Following Linear Chegg Com

Time Invariant System Question Electrical Engineering Stack Exchange

Introduction To Linear Time Invariant Dynamic Systems For Students Of Engineering Open Textbook Library

Properties Of Linear Time Invariant Systems And Various Transforms Mcgraw Hill Education Access Engineering

Linear Time Invariant Lti System Step Response Electricalworkbook

1

Ppt Concept Of Frequency In Discrete Signals Introduction To Lti Systems Powerpoint Presentation Id 3043485

Signals And Systems Analysis Net 351 Instructor Dr

Introduction To Lti Systems Youtube

2 3 Properties Of Linear Time Invariant Systems Ppt Download

Dsp Time Invariant Systems

Ppt Linear Time Invariant Systems Powerpoint Presentation Free Download Id 5500957

Linear Time Invariant System Wikipedia

Gate Ese Lession 12 Time Invariant And Time Variant System Offered By Unacademy

The Linear Time Invariant System

2

Lecture 4 Linear Time Invariant Systems Instructor Dr

Linear Time Variant Linear Time Invariant Systems Youtube

Signal And Systems Lti Systems Linear Time Invariant Systems Ppt Download

Discrete Time Linear Time Invariant Systems And Z Transforms Iam

Linear Time Invariant Systems And Their Frequency Response

Solved 2 Given The Following Systems Please Determine If Chegg Com

Dsp Time Variant Systems

Time Invariant Systems Discrete Time Signals And Systems Openstax Cnx

Properties Of Linear Time Invariant Systems And Various Transforms Mcgraw Hill Education Access Engineering

Classification Of Signals Systems Introduction To Signals A

Lti System Properties Example

Linear Time Invariant System Wikipedia

Solved 2 A Property Of Linear Time Invariant Systems Is Chegg Com

Frequency Response Descriptions For Lti Systems Youtube

1

Recall that the dierence equationy 7f3y corresponds to the above system.

As it burns tremendous amount of fuel the mass reduces quickly over short periods of time. Characterization of LTI Systems. The input and output of LTI system are related by. Linear Time-invariantLTI systems have two properties. The mass changes as it burns fuel but the change can be neglected and the system can be approximated as a time invariant system. As it burns tremendous amount of fuel the mass reduces quickly over short periods of time. Since we have completed the digital system examples in this post I am going to classify them and explain regarding various classifications of a digital system. Yn 3xn is linear since doubling it yields 2yn 6xn 2yn 32xn. Yn xn2 is not linear since 2yn 2xn2 does not reduce to yn xn2.

The mass changes as it burns fuel but the change can be neglected and the system can be approximated as a time invariant system. Classifications Of A Digital System. 24 Therefore the impulse responsehn h 0 n of an LTI system characterizes the system completely. The rocket is at the other end of this case. Most of the systems in the nature are LTI systems. In this figure x t x t and x t t 0 x t t 0 are passed through the system TI. Time-invariant systems are systems where the output does not depend on when an input was applied.